Shoodak

SHOODAK is a debayering algorithm developed by Stephan Schuh (http://www.imdb.com/name/nm0775939/).

1 Scope

The goal of the SHOODAK debayering method is to avoid the typical "digital sharpness" that we know too well from digital cameras nowadays. SHOODAK is meant to create a more natural looking image that is perceived closer to 35mm film negative as there are no sharpening effects that create contrast lines around edges. Also SHOODAK is meant to preserve the original grain/noise pattern from image sensors as much as possible. The SHOODAK process is meant to be very lightweight in terms of required processing resources.

2 Technical Details

For color reconstruction a bi-linear method plus a weighted (25% - 50% seems a reasonable range) random (or pseudo random) influence of neighboring pixels is used.

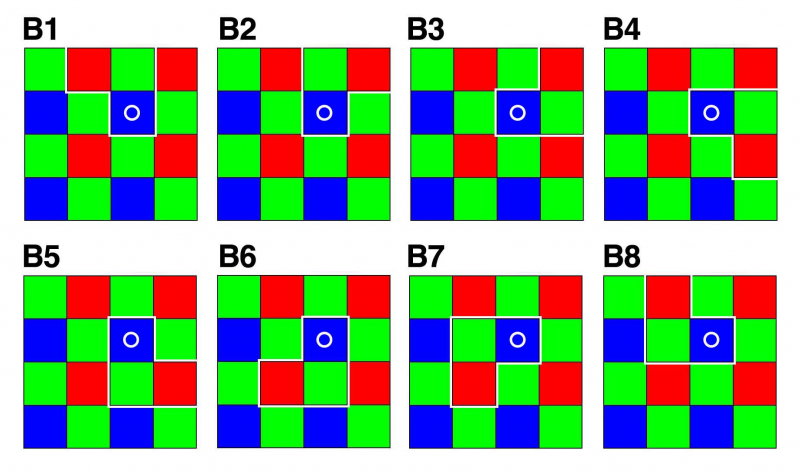
For blue pixels this creates following 8 random read out patterns (each pattern contains 1x red, 1x blue, 1x green pixel):

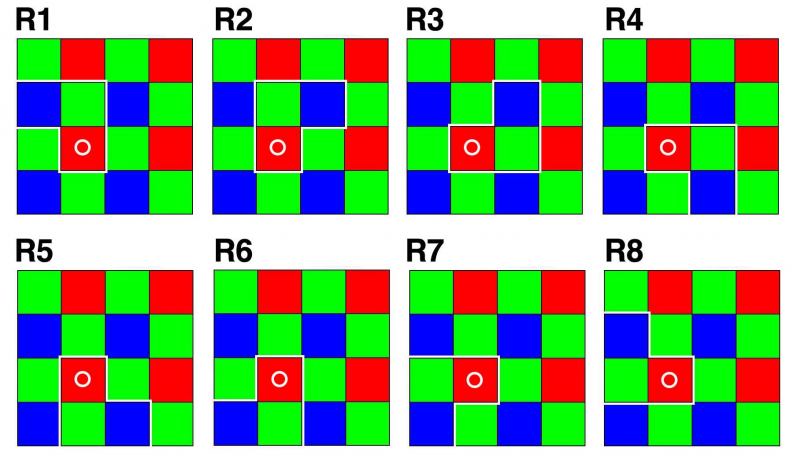
For red pixels this creates following 8 random read out patterns (each pattern contains 1x red, 1x blue, 1x green pixel):

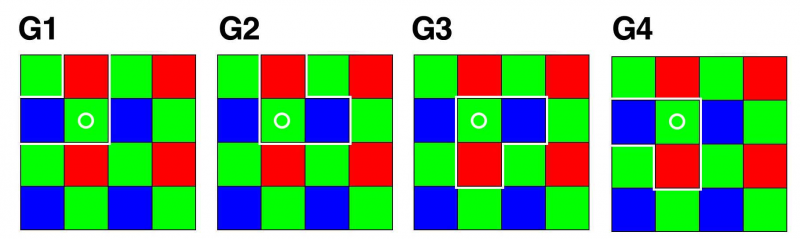
For green pixels this creates following 4 random read out patterns (each pattern contains 1x red, 1x blue, 1x green pixel):

2.1 Preventing Zipper Artifacts

A frequent problem with bi-linear debayering are so-called zipper artifacts. Visually this causes edges and lines with a zipper or chessboard look:

To counter these zipper artifacts a small percentage of the average of same-color neighboring pixels is added. Percentages below 10% have shown good results.

Neighbors for Blue, Red and Green pixels:

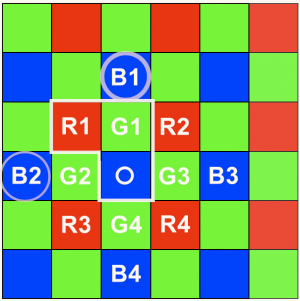
2.2 Example: Math for 1 Pixel

One random selection could look like this (parameters: 75% bi-linear, 25% random, 0% zipper reduction):

Red = (R1+R2+R3+R4) : 4 x 0.75 + R1 x 0.25

Green = (G1+G2+G3+G4): 4 x 0.75 + G1 x 0.25

Blue = O

3 References

• What is debayering article: https://www.apertus.org/what-is-debayering-article-october-2015